type
status
date
slug
summary
tags
category
icon
password
1、应用场景-背包问题
背包问题:有一个背包,容量为4磅 , 现有如下物品
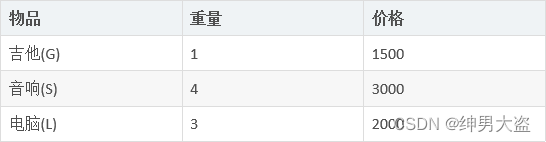
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
2、动态规划算法介绍
- 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
- 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
- 动态规划可以通过填表的方式来逐步推进,得到最优解.
3、动态规划算法最佳实践-背包问题
背包问题:有一个背包,容量为4磅 , 现有如下物品
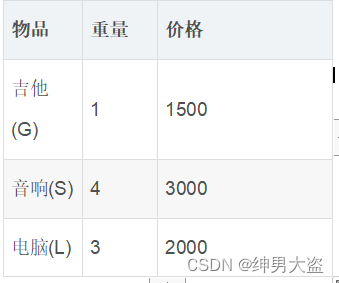
要求达到的目标为装入的背包的
总价值最大,并且重量不超出。
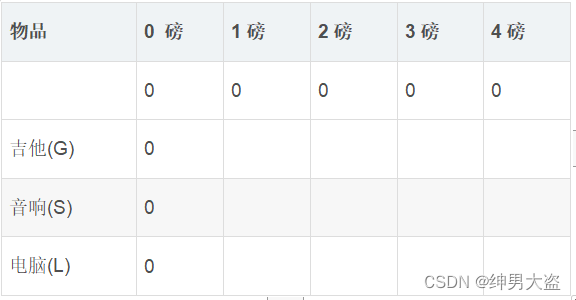
解决类似的问题可以分解成一个个的小问题进行解决,假设存在背包容量大小分为1,2,3,4的各种容量的背包(分配容量的规则为最小重量的整数倍):
例如:
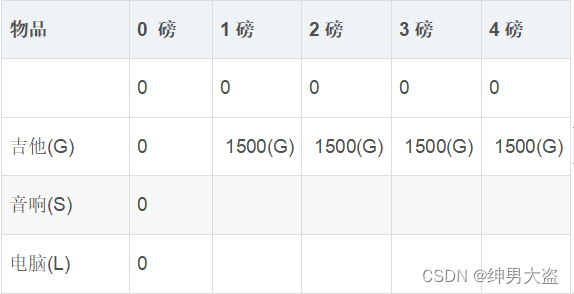
对于第一行(i=1), 目前只有吉他可以选择,所以
对于第二行(i=2),目前存在吉他和音响可以选择,所以
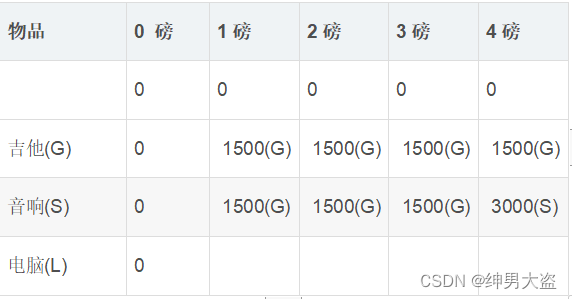
对于第三行(i=3),目前存在吉他和音响、电脑可以选择,所以

算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量,C为背包的容量。再令vi表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果: (1)vi=v0=0; //表示 填入表 第一行和第一列是0 (2) 当w[i]> j 时:vi=vi-1 // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个单元格的装入策略 (3) 当j>=w[i]时: vi=max{vi-1, v[i]+vi-1]}
当 准备加入的新增的商品的容量小于等于当前背包的容量, // 装入的方式: vi-1: 就是上一个单元格的装入的最大值 v[i] : 表示当前商品的价值 vi-1] : 装入i-1商品,到剩余空间j-w[i]的最大值 当j>=w[i]时: vi=max{vi-1, v[i]+vi-1]} :
w[i] 和 j 之间的关系 推导..
案例一:v1 = ? w[1] = 1 j = 1
w[1] = 1 j = 1 ,当j>=w[i],1>=w[1] 这时vi=max{vi-1, v[i]+vi-1]},v1=max{vi-1, v[1]+v1-1]} v1=max{v0, v[1]+v0} v1=max{0, 1500+0} v1=1500
4、动态规划算法最佳实践-背包问题-代码实现
- 作者:IT小舟
- 链接:https://www.codezhou.top/article/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%AE%97%E6%B3%95
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。

