1、应用场景-修路问题

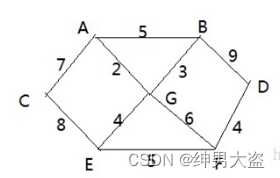
1. 有胜利乡有7个村庄(A, B, C, D, E, F, G) ，现在需要修路把7个村庄连通

2. 各个村庄的距离用边线表示(权) ，比如 A – B 距离 5公里

3. 问：如何修路保证各个村庄都能连通，并且总的修建公路总里程最短? 思路: 将10条边，连接即可，但是总的里程数不是最小. 正确的思路，就是尽可能的选择少的路线，并且每条路线最小，保证总里程数最少.

2、最小生成树

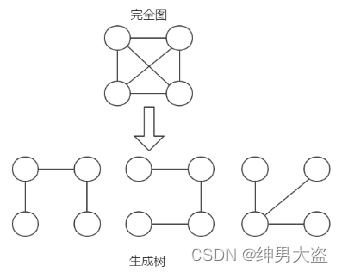
1. 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树

2. N个顶点，一定有N-1条边

3. 包含全部顶点

4. N-1条边都在图中 举例说明(如图:) 求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法

3、普里姆算法介绍

1. 普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图

2. 普利姆的算法如下:

3. 设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合

4. 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1

5. 若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1

6. 重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边 提示: 单独看步骤很难理解，我们通过代码来讲解，比较好理解.

4、普里姆算法图片解析

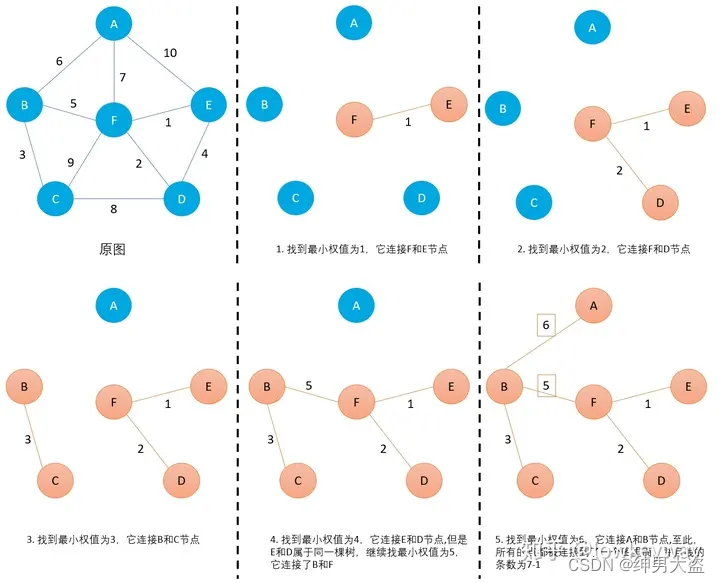
5、普里姆算法代码实现