赫夫曼编码 | 程序员小舟

type

status

date

slug

summary

1、基本介绍

赫夫曼编码也翻译为哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式, 属于一种程序算法

赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。

赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间

赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，称之为最佳编码

2、原理剖析

2.1、通信领域中信息的处理方式1-定长编码

i like like like java do you like a java // 共40个字符(包括空格) 105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97 //对应Ascii码 01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001 //对应的二进制按照二进制来传递信息，总的长度是 359 (包括空格) 在线转码工具:https://www.mokuge.com/tool/asciito16/

2.1、通信领域中信息的处理方式2-变长编码

i like like like java do you like a java // 共40个字符(包括空格)
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数 0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d 说明：按照各个字符出现的次数进行编码，原则是出现次数越多的，则编码越小，比如空格出现了9 次，编码为0 ,其它依次类推.
按照上面给各个字符规定的编码，则我们在传输 "i like like like java do you like a java" 数据时，编码就是 10010110100... 字符的编码都不能是其他字符编码的前缀，符合此要求的编码叫做前缀编码，即不能匹配到重复的编码(这个在赫夫曼编码中，我们还要进行举例说明, 不捉急)

2.3、通信领域中信息的处理方式3-赫夫曼编码

i like like like java do you like a java // 共40个字符(包括空格)
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值.(图后)

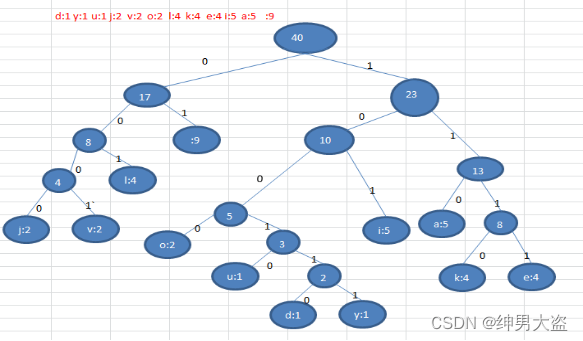
//根据赫夫曼树，给各个字符 //规定编码，向左的路径为0 //向右的路径为1 ，编码如下:
o: 1000 u: 10010 d: 100110 y: 100111 i: 101 a : 110 k: 1110 e: 1111 j: 0000 v: 0001 l: 001 : 01
按照上面的赫夫曼编码，我们的"i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的无损压缩)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
长度为： 133 说明: 原来长度是 359 , 压缩了 (359-133) / 359 = 62.9% 此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性

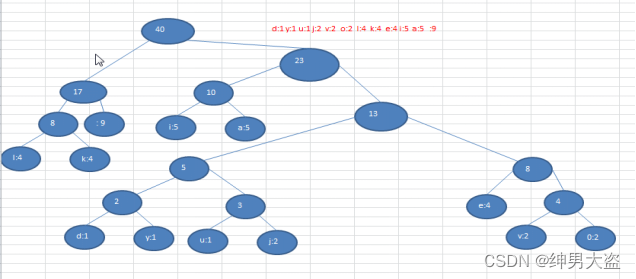
注意

, 这个赫夫曼树根据

排序方法不同

，也可能不太一样，

这样对应的赫夫曼编码也不完全一样

，但是wpl 是一样的，都是最小的, 比如: 如果我们让每次生成的

新的二叉树总是排在权值相同的二叉树的最后一个

，则生成的二叉树为:

3、最佳实践-数据压缩(创建赫夫曼树)

将给出的一段文本，比如 "i like like like java do you like a java" ，根据前面的讲的赫夫曼编码原理，对其进行数据压缩处理，形式如 "1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110 " 步骤1：根据赫夫曼编码压缩数据的原理，需要创建 "i like like like java do you like a java" 对应的赫夫曼树.

我们已经生成了赫夫曼树, 下面我们继续完成任务

生成赫夫曼树对应的赫夫曼编码 , 如下表:=01 a=100 d=11000 u=11001 e=1110 v=11011 i=101 y=11010 j=0010 k=1111 l=000 o=0011

使用赫夫曼编码来生成赫夫曼编码数据 ,即按照上面的赫夫曼编码，将"i like like like java do you like a java" 字符串生成对应的编码数据, 形式如下.1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100

输出结果

4、最佳实践-数据解压(使用赫夫曼编码解码)

使用赫夫曼编码来解码数据，具体要求是前面我们得到了赫夫曼编码和对应的编码byte[] , 即:[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28] 现在要求使用赫夫曼编码， 进行解码，又重新得到原来的字符串"i like like like java do you like a java"

5、最佳实践-文件压缩

我们学习了通过赫夫曼编码对一个字符串进行编码和解码, 下面我们来完成对文件的压缩和解压，具体要求：给你一个图片文件，要求对其进行无损压缩, 看看压缩效果如何。思路：读取文件-> 得到赫夫曼编码表 -> 完成压缩

6、最佳实践-文件压缩

具体要求：将前面压缩的文件，重新恢复成原来的文件。思路：读取压缩文件(数据和赫夫曼编码表)-> 完成解压(文件恢复)

7、赫夫曼编码压缩文件注意事项

如果文件本身就是经过压缩处理的，那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件 [举例压一个 .ppt] 赫夫曼编码是按字节来处理的，因此可以处理所有的文件(二进制文件、文本文件) [举例压一个.xml文件] 如果一个文件中的内容，重复的数据不多，压缩效果也不会很明显.